Part Three: Gross Internal Floor Area and Utilisation
Part Two of this series discussed the requirement for efficiency. However, before discussing our method in detail, it's important to understand a couple of concepts: Gross Internal Floor Area and Utilisation.
Gross Internal Floor Area
When sharing ideas about floor space, architects, engineers, and construction/estate professionals must use a standard space definition. Without this definition, there is a risk of misunderstandings.
Gross Internal Floor Area (GIFA) refers to the internal area (we will use square metres - m2) of a building or a series of buildings. This is sometimes called the Gross Internal Area (GIA); there’s no real difference. This term is applied to any building type, not just FE/HE (see below).
The GIFA is measured at each level, starting at the internal face of external perimeter walls. This means it includes all internal space, including the space taken up by internal walls and columns.
Small voids (within stairwells, lift wells, and ducts) are included in the GIFA at every level. Larger voids like Atria are counted only at their lowest level. GIFA usually excludes roof terraces, external covered spaces, and external stairways.
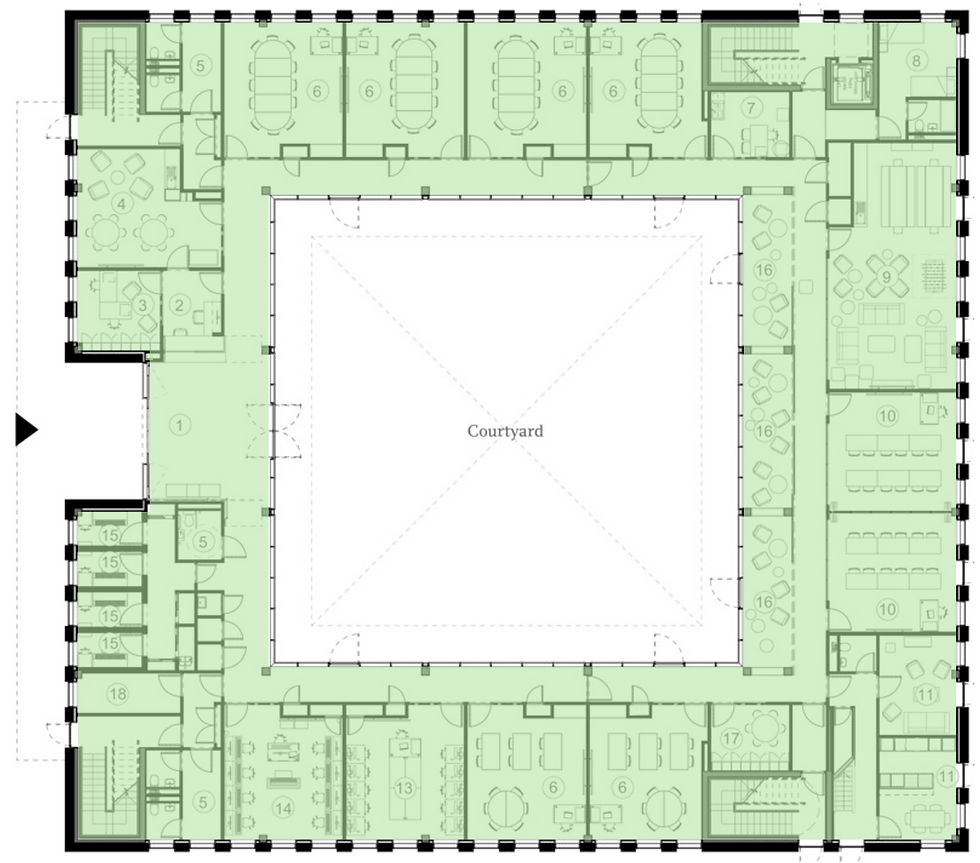
Gross Internal Floor Space (GIFA) shaded green: The King’s School International College, Canterbury (Walters & Cohen Architects)
The Method: Bottom-Up
Our last post identified the guiding principle of 'quality before quantity'. There should be sufficient space, not just teaching but also support spaces, to make the building both functional and pleasurable. At the same time, we should avoid excess space, which can be both financially and environmentally damaging.
As noted in our last post in this series, some (top-down) approaches set an overall GIFA using an allowance per student. This allowance is based on a general understanding of what a particular subject or qualification needs. So, if the allowance per student is 8m2 and the institution teaches 1,000 students, then the GIFA will be 8,000m2. The overall GIFA must then be shared, via whatever means, between various space types: teaching, study space, social, dining, etc.
Our method works in reverse (bottom-up): It notes all the anticipated activities within the building and identifies appropriate space for each. We start with teaching spaces before moving on to support spaces (and research spaces in some HE environments) and then ancillary spaces. The sum of all these spaces will be the recommended Gross Internal Floor Area (GIFA).
This approach responds to the number of students and staff and how the curriculum will be delivered. It may result in more or less GIFA than a top-down method.

Introducing Utilisation
Of course, we need to apply a reasonableness test, or a bottom-up method, that "notes all the anticipated activities", might result in a very long list of 'nice to have' teaching spaces, and the GIFA might be excessive.
So, when considering teaching space, we want to be sure that it will be used regularly.
But we also need to ensure that there is sufficient space to meet anticipated demand.
It's about balance.
For each teaching space, we need to start with two questions:
What is the anticipated demand for a space type (classrooms, labs, studios, etc.)?
What utilisation rate should we look to achieve?
A Simple Example
A college teaches 400 students in regular classrooms for ten hours per week each. The same students might also spend time in other teaching environments, but we will focus on standard classrooms here. This scenario means a weekly demand for classrooms of 4,000 'student hours' (400 x 10 = 4000).
The college delivers its teaching over a 40-hour week. So, on average, 100 students will be taught at any time (4000/40 = 100). Therefore, if attendance was spread totally evenly over the 40 hours, we would need 100 classroom workplaces to seat everyone. Note that we have yet to consider how many classrooms we need, just the total number of workplaces.
So, 100 classroom workplaces would mean 100% 'workplace utilisation' (all workplaces, aka seats, would be full over the entire 40-hour period).
However, let's say some of the teaching staff do not work on Fridays (in any case, lessons on Friday afternoons are poorly attended). In reality, the 4000 'student hours' will be delivered unevenly; there will likely be over 200 students being taught on Monday morning at 11 am, whereas numbers may not exceed 50 on Friday afternoon.
Furthermore, class sizes vary. Timetabling to exactly match class sizes with room sizes is impossible. Inevitably, some seats will be empty during lessons (as, say, classes of 18 to 25 are timetabled into rooms with 25 seats).
In reality, for a variety of reasons, 100% workplace utilisation is never achieved.
Therefore, 100 workplaces are insufficient in this example. We need more workplaces to account for the inevitable unevenness of lesson provision and group sizes.
So, if a workplace utilisation of 50% is more realistic, we require 200 workplaces. Since:
Demand/Supply = Workplace Utilisation.
Average 100 attendees (demand)/200 seats (supply) = 50%
But is 50% utilisation reasonable?
Next Time
The next MabelPost will examine what realistic utilisation rates suit different teaching environments.
Of course, proposing a number of workplaces is only half the exercise. We will also examine ‘workplace standards’ (the m2 area per workplace) for different teaching environments.
We can then use these utilisation rates and workplace standards, alongside curriculum planning, to propose a teaching space allocation for any further or higher education scenario.
We can also consider how this allocation can be subdivided into individual spaces.
